 ForgotMyCode
ForgotMyCode
| Home |
Advanced Algorithm Analysis
#2: Advanced Sums
Sum to integration
Take a non-decreasing function $f(x)$.
We can estimate lower and upper bound using integration as follows:
\[\int_{0}^{n}f(x)dx \leq \sum_{x=1}^{n}f(x) \leq \int_{1}^{n+1}f(x)dx\]It comes from the property of the function being non-decreasing.
A little visual proof, consider the function (non-decreasing when $x \geq 0$) and the green blocks representing its sum from 1 to $n$.
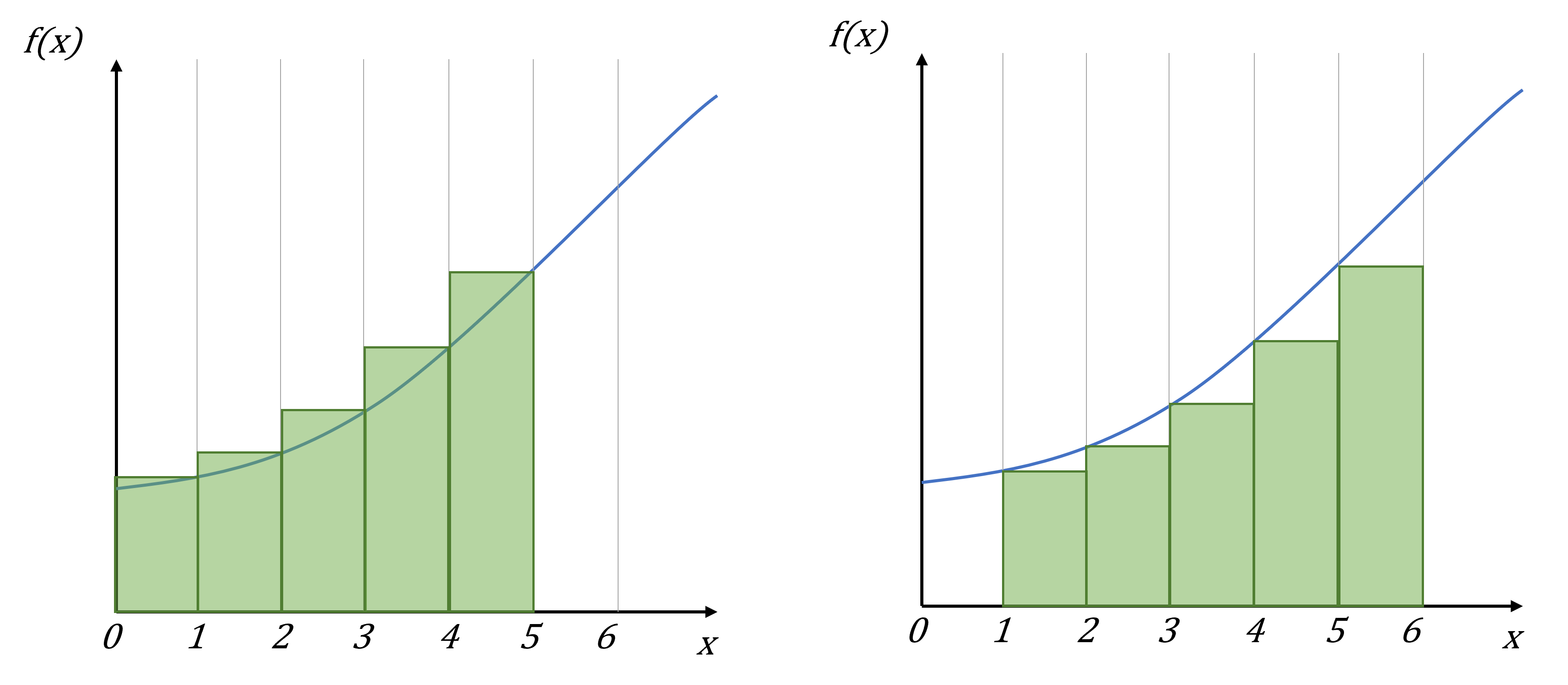
In this example, $n = 5$.
The green rectangles represent the sum. Their width is 1 and their height is $f(x)$.
It should be possible to see that the sum is smaller that the area under $f(x)$ in the interval $\left \langle 1, n + 1 \right \rangle = \left \langle 1, 6 \right \rangle$, but larger than the area under $f(x)$ in the interval $\left \langle 0, n \right \rangle = \left \langle 0, 5 \right \rangle$.
Similarly for non-increasing function $f(x)$:
\[\int_{1}^{n+1}f(x)dx \leq \sum_{x=1}^{n}f(x) \leq \int_{0}^{n}f(x)dx\]Can you prove it mathematically?
Arithmetic sequence
Just a little reminder, arihmetic sequence is a sequence $a_{1}, … , a_{n}$ such that $a_{i + 1} = a_{i} + d$.
The important takeaway is we can calculate (finite) sum of such sequence using this formula:
\[\sum_{i=1}^{n}a_{i}=n\frac{a_{1} + a_{n}}{2}\]Geometric sequence
Another little reminder, geometric sequence is a sequence $g_{1}, … , g_{n}$ such that $g_{i + 1} = q g_{i} $.
The important takeaway is we can calculate (finite) sum of such sequence using this formula:
\[\sum_{i=1}^{n}g_{i} = \left\{\begin{matrix} g_{1}\frac{q^{n} - 1}{q - 1} & q \neq 1\\ g_{1}n & q = 1 \end{matrix}\right.\]and
\[\sum_{i=1}^{\infty }g_{i} = \frac{g_{1}}{1 - q}, \left | q \right | < 1\]